排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

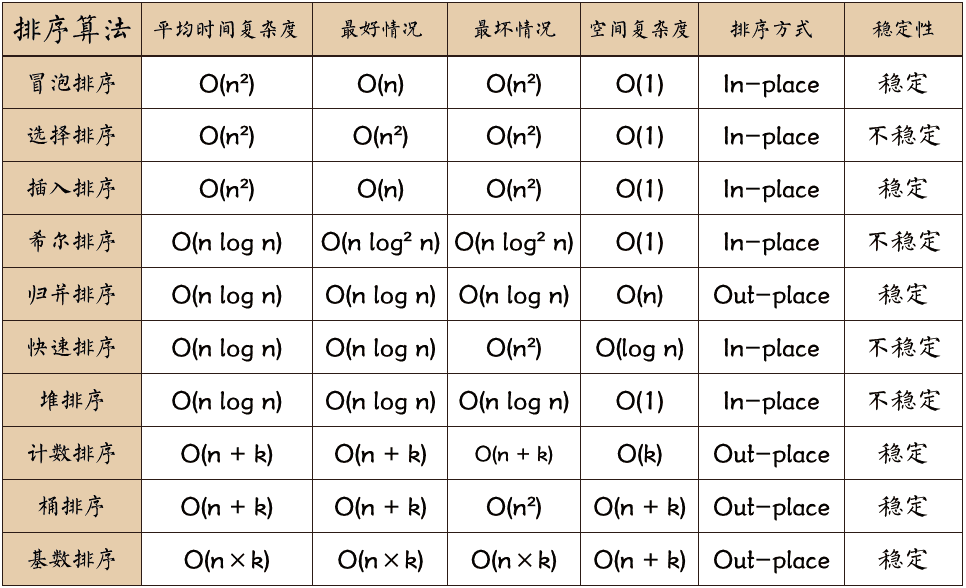
用一张图概括：

名词解释：

• n：数据规模
• k：“桶"的个数
• In-place：占用常数内存，不占用额外内存
• Out-place：占用额外内存
• 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

内部排序	描述
冒泡排序	（无序区，有序区） 从无序区通过交换找出最大元素放到有序区最前端。
选择排序	（无序区，有序区） 从无序区选择一个最小的元素放到有序区的末尾。比较多，交换少
插入排序	（无序区，有序区） 把无序区的第一个元素插入到有序区合适的位置。比较少，交换多
希尔排序	通过比较相距一定间隔的元素来进行（每一定间隔取一个元素组成子序列），各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟排序为止。
归并排序	把数组从中间分成前后两部分，分别排序，再将排好序的两部分合并。
快速排序	（小数，基准，大数） 随机一个元素作为基准数，将小于基准的元素放在基准之前，大于基准的放在基准之后，再分别对小数区与大数区进行排序。
堆排序	（大顶堆，有序区） 取出堆顶元素放在有序区，再恢复堆。
计数排序	统计小于等于该元素值的元素个数i,于是该元素就放在目标数组的索引i位（i>=0）。
桶排序	将值为i的元素放在i号桶，最后依次把桶里元素倒出来。
基数排序	一种多关键字的排序算法，可用桶排序实现。

1. 冒泡排序（Bubble Sort）

冒泡排序（Bubble Sort）是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

图（Graph）。和树比起来，这是一种更加复杂的非线性表结构，由顶点和连接每对顶点的边所构成的抽象网络就是图。

图的定义：图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是顶点的集合，E是边的集合。

图中的元素叫做顶点（vertex）。顶点与其他顶点建立的连接关系叫做边（edge）。跟顶点相连接的边的条数叫做顶点的度（degree）。

如果图中任意两个顶点之间的边都是无向边（边没有方向），则称该图为无向图（Undirected graphs）。 以此类推，把边有方向的图称为有向图（Directed graphs）。

• 完全图：
  • ①无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。
  • ②有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。
• 当一个图接近完全图时，则称它为稠密图（Dense Graph），而当一个图含有较少的边时，则称它为稀疏图（Spare Graph）。

1. 图的存储方式

图的两个主要的存储方式：邻接矩阵和邻接表。 邻接矩阵存储方法的缺点是比较浪费空间，但是优点是查询效率高，而且方便矩阵运算。 邻接表存储方法中每个顶点都对应一个链表，存储与其相连接的其他顶点。尽管邻接表的存储方式比较节省存储空间，但链表不方便查找，所以查询效率没有邻接矩阵存储方式高。针对这个问题，邻接表还有改进升级版，即将链表换成更加高效的动态数据结构，比如平衡二叉查找树、跳表、散列表等。

堆的两点要求：

• 堆是一个完全二叉树；
• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。
  • 对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做大顶堆。
  • 对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做小顶堆。

• 完全二叉树：除最后一层外，其他层的节点都满；并且最后一层的节点从左到右是连续排列，中间没有断开，空位都在右边。
• 在构建完全二叉树的时候，新加入的节点在最后一层从左往右依次排列，直到排满为止。

有两种方法存储一棵二叉树，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。 堆是一种完全二叉树，最常用的存储方式就是基于数组的顺序存储法。

1. 基于数组的顺序存储法。

如下图，我们把根节点存储在数组下标 i=1 的位置，那左子节点存储在下标 2*i = 2 的位置，右子节点存储在 2*i+1 = 3 的位置。以此类推，B节点的左子节点存储在 2*i = 2*2 = 4 的位置，右子节点存储在 2*i+1 = 2*2+1 = 5 的位置。

平衡二叉查找树其实有很多，比如，红黑树（Red-Black Tree，简称 R-B Tree）、伸展树（Splay Tree）、树堆（Treap）等，但是我们提到平衡二叉查找树，听到的基本都是红黑树，它是一种不严格的平衡二叉查找树。 红黑树是一种含有红黑节点并能自平衡的二叉查找树。它必须满足下面性质：

1. 每个节点要么是红色，要么是黑色；
2. 根节点是黑色的；
3. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
4. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
5. 任意一节点到每个叶子节点的路径，都包含相同数目的黑色节点；

1. 红黑树的平衡特征

红黑树与AVL树类似，都在添加和删除的时候通过旋转操作保持二叉树的平衡，以求更高效的查询性能。

AVL树（得名于发明者G. M. Adelson-Velsky 和 E. M. Landis）本质上是一棵带有平衡条件的二叉搜索树。 AVL树具有以下2个性质：

1. 左子树和右子树的深度之差的绝对值不超过1；
2. 左子树和右子树全都是 AVL树。

其中为了度量左右子树的深度之差，我们引入平衡因子(BF)的概念。

平衡因子： 某个节点的左子树的高度减去右子树的高度得到的差值。

对于一棵 AVL树，里面的所有节点的平衡因子只能取值于-1、0、1，否则，AVL树将是不平衡的并且需要平衡调整。

1. AVL 树平衡调整

二叉树的平衡化有两大基础操作： 左旋（rotate left）和右旋（rotate right）。

树：树是一种非线性的数据结构，一棵树是n（n>=0）个节点的集合。 用来连接相邻节点之间的关系，我们叫做“父子关系”。 我们把没有父节点的节点叫做根节点，节点的上一层节点是其父节点，下一层节点是其子节点，拥有相同父节点的子节点之间互称为兄弟节点。

• 树的三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。
  • 节点的高度：节点到叶子节点的最长路径（边数）
  • 节点的深度：根节点到这个节点所经历的路径（边数）
  • 节点的层数：节点的深度 +1
• 树的高度：根节点的高度。

1. 二叉树

二叉树：每个节点最多有两个子节点，分别是左子节点和右子节点。 二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。